数组算法

一些算法举例

数组

接雨水问题

题目

leetcode-42：给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水，如下所示：

rain

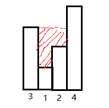
上图中，盛水量为3.

示例

输入：height = [3,1,2,4]
输出：3

思路

暴力法

每个i位置，都前后遍历，从i位置向前和向后遍历，找到前后max值较小的减去当前i位置的值就是能装的水，要是前或者后没有找到比i位置小的，那么就不能装水，复杂度为O(n2)

  //柱状图接水(暴力法)
  func getWaterByViolence(src: [Int]) -> Int {
      var rt = 0
        
      if src.isEmpty || src.count < 3 {
          return rt
      }
        
        
      for i in 1..<src.count-1 {
          var leftMax = src[0]
            
  //        获取作则最大值
          for j in 0..<i {
              if src[j] > leftMax {
                  leftMax = src[j]
              }
          }
            
  //        获取右侧最大值
          var rightMax = src[src.count-1]
            
          for k in (i+1...src.count-1).reversed() {
              if src[k] > rightMax {
                  rightMax = src[k]
              }
          }
            
  //        左右两个大值中的较小者和src[i]的差值就是当条柱状图所能储水的值
  //        且如果他们都比src[i]小的话就储不了水
          rt += max(0, min(leftMax, rightMax) - src[i])
      }
        
      print("\(src)'s 柱状图接水(暴力法) is \(rt)")
    
      return rt
  }

控制台

let _ = getWaterByViolence(src: [3, 1, 2, 4])

[3, 1, 2, 4]’s 柱状图接水(暴力法) is 3

双指针法

定义一个双指针，分别为左右指针，分别指向arr[1]和arr[count-2]，因为第一个和最后一个肯定不能储水，同时定义2个最值，leftMax和rightMax分别为第二个元素和倒数第二个元素。当左最值小于右最值时，右滑左指针，左指针上能储的水就是：左最值＞左指针，相减，左最值<左指针，不减，更新左最值；同样的逻辑对于左最值大于右最值时，也来一遍。时间复杂度为O(n),空间复杂度为O(1)

          //柱状图接水(左右指针法)，时间复杂度O(n2)，空间复杂度O(1)
      func getWaterBy2P(arr: [Int]) -> Int {
          var rt = 0
            
          if arr.isEmpty || arr.count < 3 {
              return rt
          }
            
          var leftMax = arr[0]
          var rightMax = arr[arr.count-1]
            
          var leftP = 1
          var rightP = arr.count-2
            
          while leftP <= rightP {
              if leftMax <= rightMax {
      //            rt += leftMax-arr[leftP] > 0 ? leftMax-arr[leftP] : 0
                  rt += max(0, leftMax-arr[leftP])
                  leftMax = max(leftMax, arr[leftP])
                    
                  leftP+=1
              } else {
      //            rt += rightMax-arr[rightP] > 0 ? rightMax-arr[rightP] : 0
                  rt += max(0, rightMax-arr[rightP])
                  rightMax = max(rightMax, arr[rightP])
                    
                  rightP -= 1
              }
          }
            
          print("\(arr)'s 柱状图接水(左右指针法) is \(rt)")
        
          return rt
      }

控制台

let _ = getWaterBy2P(arr: [3, 1, 2, 4])

[3, 1, 2, 4]’s 柱状图接水(左右指针法) is 3

二分插入法

给出一个有序数组（入从小到大），将指定的数字插入合适的位置，返回index。

示例

输入：[1, 2, 3, 4, 6, 7, 8, 9, 10, 10, 11, 18, 76]，14
输出：11

思路

上下边界，二分判断，直到下边界>=上边界，退出循环

解法

func binarySearch(insert target: Int, into src: [Int]) -> Int {
    var left=0, right=src.count-1
    
    while left<=right {
        let mid=(left+right)/2
        let midValue=src[mid]
        
        if target==midValue {
            return mid
        } else if target>midValue {
            left=mid+1
        } else {
            right=mid-1
        }
    }
    
    print("\(target) Should insert at Index: \(left)")
    return left;
}

测试

let _=binarySearch(insert: 14, into: source)

14 Should insert at Index: 11

寻找中间数

给出一个无序数组，求出一个数，使得其左边的数都小于它，右边的数都大于等于它。要求时间复杂度为n

示例

输入：[4,3,2,7,9,10,11,10]
输出：7,9

思路

两次遍历，第一次遍历，记录下每个位置和它之后的那个元素的最小值（当然这个最小值会一直更新，所以这一次遍历完，就是整个数组的最小值），需要一个n的数组，存放的是这个位置和它后面一个位置的较小值，当然如果已经遇到了，最小值，因为会和最小值进行判断，所以后续这个新的数组里存放的都是这个最小值了。

第二次遍历是正常的从左向右遍历，寻找左边大且比右边小的数，也会记住一个最大值。

解法

func findTheMidNumber(_ data: [Int]) -> [Int] {
  var res = [Int]()

  if data.count == 0 {return res}
  if data.count <= 2 {return res}

  var rightMin = [Int](repeating: 0, count: data.count)
  var r_min = data[data.count-1]

  //从右往左，寻找每个位置及其之后的最小数
  for i in (0..<data.count).reversed() {
    if data[i] < r_min {
      r_min = data[i]
    }
    rightMin[i] = r_min
  }

  //从左往右，寻找左边大且比右边小的数
  var l_max = data[0]
  for i in 0..<data.count-1 {
    if data[i] > l_max {
      l_max = data[i]
      if data[i] < rightMin[i+1] {
        res.append(data[i])
      }
    }
  }
  print(res)
  return res
}

测试

_ = findTheMidNumber([4,3,2,7,9,10,11,10])

[7, 9]

三数之和

一个包含n个整数的数组nums，判断nums中是否存在三个元素a，b，c，使得a+b+c=0？请找出所有满足条件且不重复的三元组

注意：不可以包含重复的三元组

示例

输入：nums=[-1,0,1,2,-1,-4]
输出：[[-1,0,1], [-1,-1,2]]

思路

除非三个数全是0，否则肯定会有正数和负数，所以假定选择一个数，然后再去找另外两个数，这样只要找到两个数且和为第一个选择的数的相反数。

从小到大排序
循环
如果最小的数大于0，直接结束（因为必须要有负数）

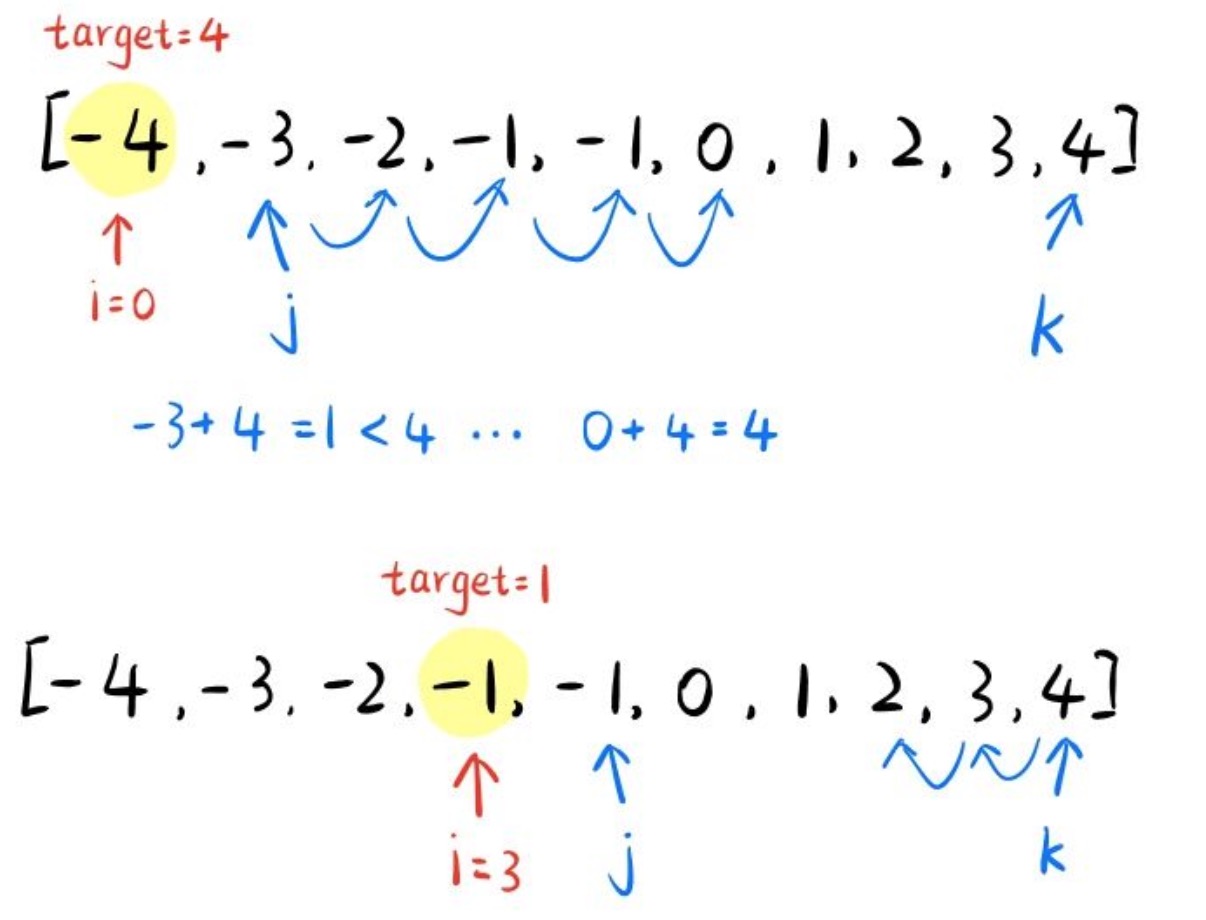
sort_algorithm

相当于两数之和问题：a+b=target，因为是排好序的，选定了i，那么j+k需要是i的相反数，如果j+k<target，则j++,否则k–，j和k是右边数组的首末两端

解法

func threeSum(_ nums: [Int])->[[Int]]? {
  var tempNums = nums

  if nums.count <= 0 {return nil}
  //排序
  insertSort(arr: &tempNums)
  if tempNums[0] > 0 {return nil}

  var res = [[Int]]()

  for i in 0..<tempNums.count {
    let target = -tempNums[i]

    var j = i+1
    var k = tempNums.count-1

    while k-j > 0 {
      let numj = tempNums[j]
      let numk = tempNums[k]

      if numj+numk < target {
        j += 1
      } else if numj+numk > target {
        k -= 1
      } else {
        //找到，返回i，j，k
        res.append([tempNums[i],numj,numk])
        break
      }
    }
  }

  return res
}

测试

let res = solution.threeSum([-1,0,1,2,-1,-4])

结果

[[-1, -1, 2], [-1, 0, 1]]

岛屿最大面积

给定一个包含了一些 0 和 1 的非空二维数组 grid 。

一个岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)

示例

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

解法

func dfs(_ i: Int,_ j: Int,_ m: Int,_ n:Int,_ grid: inout [[Int]],_ tempArea: inout Int) -> Int {
  if i<0 || i>=m || j<0 || j>=n || grid[i][j] == 0 {
    return tempArea
  }
  grid[i][j] = 0
  tempArea += 1
  tempArea = dfs(i+1, j, m, n, &grid, &tempArea)
  tempArea = dfs(i-1, j, m, n, &grid, &tempArea)
  tempArea = dfs(i, j+1, m, n, &grid, &tempArea)
  tempArea = dfs(i, j-1, m, n, &grid, &tempArea)
  return tempArea
}

func maxAreaOfIsland(_ grid: [[Int]]) -> Int {
  var tempGrid = grid
  var area = 0
  let m = tempGrid.count
  var n = 0
  var islandMax = 0
  for i in 0..<m {
    n = tempGrid[i].count
    for j in 0..<n {
      area = 0
      area = dfs(i, j, m, n, &tempGrid, &area)
      islandMax = max(islandMax, area)
    }
  }
  return islandMax
}

最长上升子序列（非连续）

给定一个未经排序的整数数组，找到最长递增子序列

示例

输入：10，9，2，5，3，7，101，18，20
输出：2，3，7，18，20

思路
- 动态规划的方式：第一层循环省不了：for i:0->n-1。
  - 状态定义：DP[i]表示从头到第i个元素，且第i个元素要被选上的最长子序列的长度。DP[i]不是最后一个的长度，实际上是max{DP[0],DP[1]…DP[i-1]}+1，因为i必须要被选上。
  - 状态转移方程：for i:0->n-1 {for j:0->i-1} 两层循环，时间复杂度是O(\(n^2\))
DP[i]=max{DP[j]}+1, j:0->i-1 且a[j]<a[i]
- 一个巧妙的方法：上述方式，只能第二层循环才能加速。一般来说第一遍for i->n-1(n),第二遍for j->i-1(n).这里可以加速的是第二个循环，因为第一个循环肯定是不能加速的，所以只能加速第二个循环。可以维护一个数组LIS（最后的结果数组），一开始数组是空的，当第一个数10进来，毫无疑问，它就是最长递增子序列，9进来的时候，如果它比10大则直接append，否则用二分查找法去找到数组中比它大的最小的数，替换掉，因为我们相当于要不断让更小的数进来，所以很好理解。这个复杂度是logn的，所以整体是nlogn的时间复杂度。

DP方式：

实现

   //寻找最长上升子序列（不需要连续),10，9，2，5，3，7，101，18，20->2,3,7,18,20
   func findLongestIncrementSequenceWithDP(src: [Int]) -> Int {
       if src.count<=0 {
           return 0
       }
            
       var rls=1
            
       var DP = Array.init(repeating: 1, count: src.count)
            
       for i in 1..<src.count {
           for j in 0..<i {
               if src[j]<src[i] {
                   DP[i]=max(DP[i], DP[j]+1)
               }
           }
                
           rls=max(rls, DP[i])
       }
            
       print("\(src)'s LIS count is \(rls)")
       return rls
   }

结果

let _=findLongestIncrementSequenceWithDP(src: [10,9,2,5,3,7,101,18,20])

[10, 9, 2, 5, 3, 7, 101, 18, 20]’s LIS count is 5

巧妙方式

实现

 //寻找最长上升子序列（不需要连续),10，9，2，5，3，7，101，18，20->2,3,7,18,20
 func findLongestIncrementSequence(src: [Int]) -> [Int] {
     if src.count<=0 {
         return []
     }
          
     var rls=[Int]()
          
     for i in 0..<src.count {
         let index=binarySearch(insert: src[i], into: rls)
              
         rls.insert(src[i], at: index)
              
         if index+1<rls.count {
             rls.remove(at: index+1)
         }
     }
          
     print("\(src)'s LIS is \(rls)")
     return rls
 }

其中binarySearch是笔者自己实现的二分查找，找到应该插入的位置，所以后续还要删除原来的数字，等于是替换。如果标准库有对应的low_bounder方法，则不需要自己实现。

结果

let _=findLongestIncrementSequence(src: [10,9,2,5,3,7,101,18,20])

[10, 9, 2, 5, 3, 7, 101, 18, 20]’s LIS is [2, 3, 7, 18, 20]

最长连续递增序列

给定一个未经排序的整数数组，找到最长且连续的递增序列，并返回该序列的长度。

示例

输入：[1,3,5,4,7]
输出：3
解释：最长递增序列是[1,3,5], 长度为3

输入：[2,2,2,2]
输出：1
解释：最长连续递增序列是[2], 长度为1

注：数组长度不超过10000

思路
- count 为当前元素峰值，ans为最大峰值
- 初始化 count=1
- 从0位置开始遍历，遍历是根据前后元素状态判断是否递增，递增则count++，递减count=1
- 如果count>ans，则更新ans
- 直到循环结束
解法

func findLengthOfLCIS(_ nums: [Int])->Int {
  if nums.count <= 1 {return nums.count}
  var ans = 1
  var count = 1

  for i in 0..<nums.count-1 {
    if nums[i+1] > nums[i] {
      count += 1
    } else {
      count = 1
    }

    ans = count>ans ? count : ans
  }

  return ans
}

结果

print(solution.findLengthOfLCIS([1,3,5,4,7]))

3

数组中的第K大的元素

在未排序的数组中找到第k大的元素。

示例

输入： [3,2,1,5,6,4], k=2
输出：5

输入： [3,2,3,1,2,4,5,5,6], k=4
输出：4

假设k总是有效的，且1<=k<=数组长度

思路

改进快速排序算法，求得第k大的元素，不需要将快速排序完全进行完，只需要进行一遍的递归，如果q刚好是第k大，则打完收工。

解法

//寻找pivot的函数
func partition(arr: inout [Int], left: Int, right: Int) -> Int {
  let pivot = left
  var index = pivot+1
  for i in index...right {
    if arr[i] < arr[pivot] {
      arr.swapAt(i, index)
      index+=1
      //i和index都更新，以pivot为分隔，两边都冒泡，后面再将假设的pivot替换为真正的pivot，然后继续递归
    }
  }
  //此处相当于pivot需要更新
  arr.swapAt(pivot, index-1)
  return index-1
}

func findKthLargest(_ nums: inout [Int], _ k: Int) -> Int {
  return quickSelect(&nums, 0, nums.count-1, nums.count-k)
}

func quickSelect(_ a: inout [Int], _ l: Int, _ r: Int, _ index: Int) -> Int {
  let q = partition(arr: &a, left: l, right: r)
  if q == index {
    return a[q]
  } else {
    return q<index ? quickSelect(&a, q+1, r, index) : quickSelect(&a, l, q-1, index)
  }
}

结果

var nums = [3,2,3,1,2,4,5,5,6]

let r10 = solution.findKthLargest(&nums, 4)

4

最长连续增序列

给定一个未排序的整数数组，找出最长连续增序列的长度。

要求算法复杂度O（n）

示例

输入：[100,4,200,1,3,2]
输出：4
解释：最长连续序列是[1,2,3,4]。长度为4

思路

使用hashmap来保存数组中已经遍历过的元素，key对应元素的值，value表示该元素所在的连续子数组的长度。如果hash中存在此元素，则遍历下一个元素。如果不存在，则看hashmap中是否存在在此元素的前一个元素，比如如果遍历到5时，看看hash中是否存在4，如果存在则取该连续子数组的子一个元素，将它value值+1，并将该元素放到hashmap中，value值与第一个元素值相同，都表示该连续子数组的长度。如果hashmap中存在的该元素遍历到5时，hashmap中是否存在6，将次元素加入到最后一个连续的子数组中，并且和2中一样，找到子数组的第一个和最后一个元素，将它们的value值更新为子数组的长度。

swift解法简单，先排好序，然后判断i-1的值+1是否等于i的值，是的话，则继续向后，否则，当前和记录的最大值比较，currentstreak=1初始化

解法

func longestConsecutive(_ nums: [Int]) -> Int {
  guard nums.count > 0 else { return 0 }
  let nums = nums.sorted(){$0 < $1}
  
  var longestStreak = 1
  var currentStreak = 1
  for i in 1..<nums.count {
    if nums[i] != nums[i - 1] {
      if nums[i - 1] + 1 == nums[i] {
        currentStreak += 1
      } else {
        longestStreak = max(longestStreak, currentStreak)
        currentStreak = 1
      }
    }
  }
  return max(longestStreak, currentStreak)
}

按频率对整数数组进行排序

应该按频率对数组排序，如果相同的频率则对整数排序

示例

输入：1 1 1 1 1 2 1 2 3 3 3 3 3
输出：1 1 1 1 1 1 3 3 3 3 3 2 2

思路

用hashmap存放数字出现的次数，然后对hashmap的value进行排序

代码实现：

func sortFrequencyArray(source: [Int]) -> [Int] {
  if source.count <= 1 {
    return source
  }

  //key是数字，value是出现的频率
  var hashTable: Dictionary<Int, Int> = [Int:Int]()
  for i in 0..<source.count {
    let key: Int = source[i]

    if hashTable.keys.contains(key) {
      //更新数值
      var value = hashTable[key]
      value! += 1
      hashTable[key] = value
    } else {
      hashTable[key] = 1
    }
  }

  let values = hashTable.sorted{
    if $0.1 == $1.1 {
      //如果value（频率）相等，则按照key倒序
      return $0.0 > $1.0
    }

    //如果value（频率）不等，则按照value倒序
    return $0.1 > $1.1
  }

  var result: [Int] = [Int]()

  for i in 0..<values.count {
    for _ in 0..<values[i].1 {
      result.append(values[i].0)
    }
  }

  return result
}

测试

let array6 = [8,8,8,8,8,8,8,8,8,8,8,8,8,7,7,1,1,6,6,1,1,1,2,1,2,4,4,3,3,5,5]
let array7 = solution.sortFrequencyArray(source: array6)
print(array7)

结果

[8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 1, 1, 1, 1, 1, 1, 7, 7, 6, 6, 5, 5, 4, 4, 3, 3, 2, 2]

上篇字符串算法

下篇链表算法