一些算法举例
排序算法
首先看一张图:
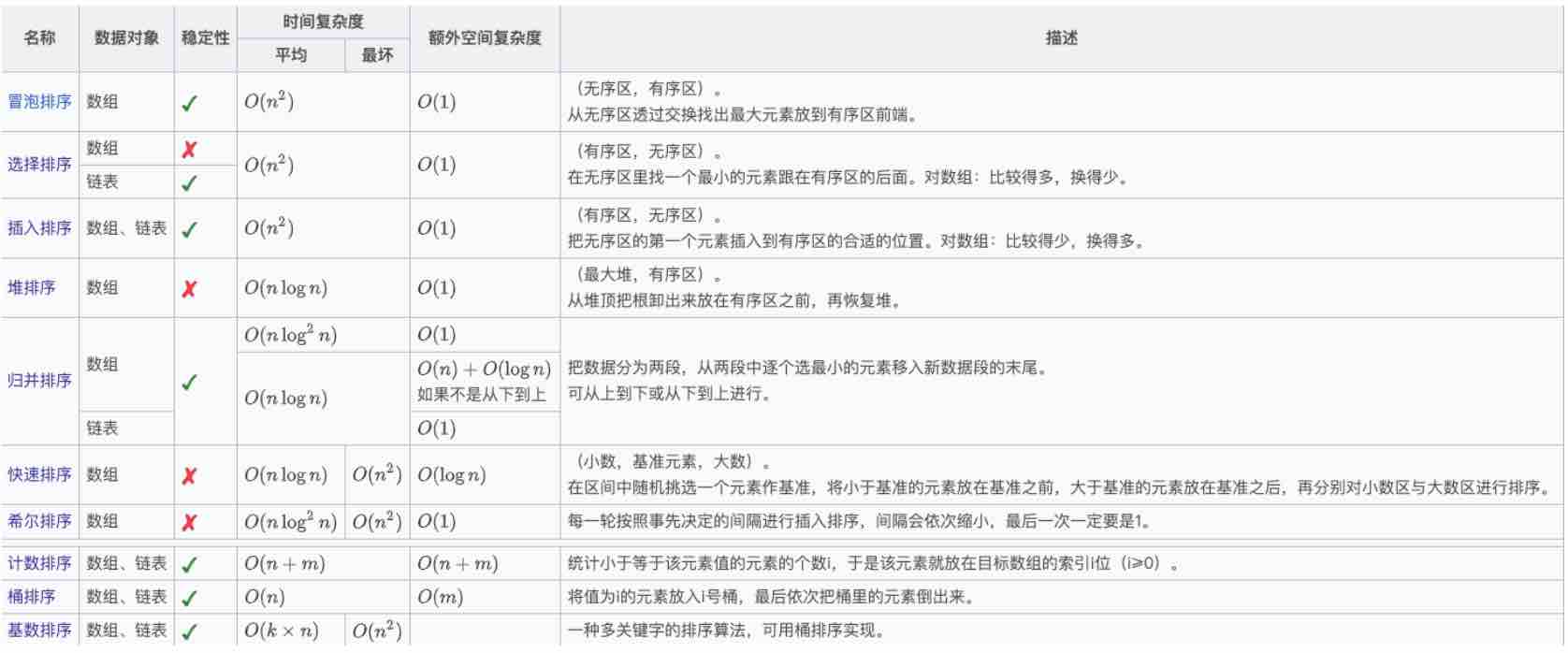
这里就不多解释了,下面抽几个排序简单讲下。
成功
信息
Warning Text.
Error Text.
success info warning error
冒泡排序
- 算法步骤
比较相邻的元素。如果第一个比第二个大,就交换他们两个。 对每一对相邻元素作同样的工作,从开始第一队到结尾的最后一对。这步做完后,最后的元素会是最大的数。 针对所有的元素重复以上的步骤,除了最后一个。 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
- 动图演示
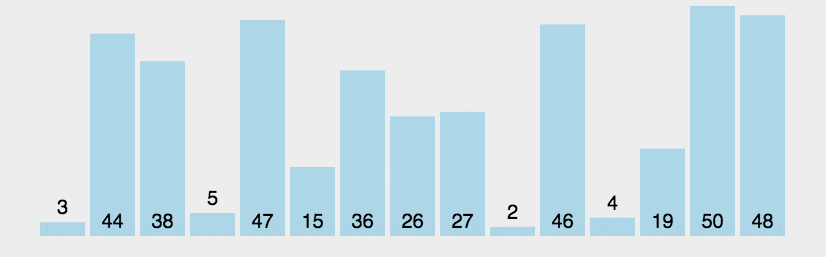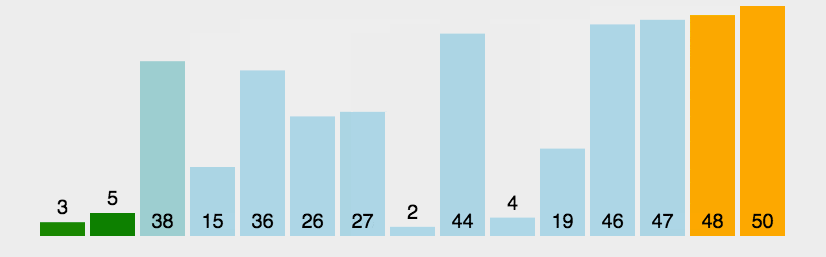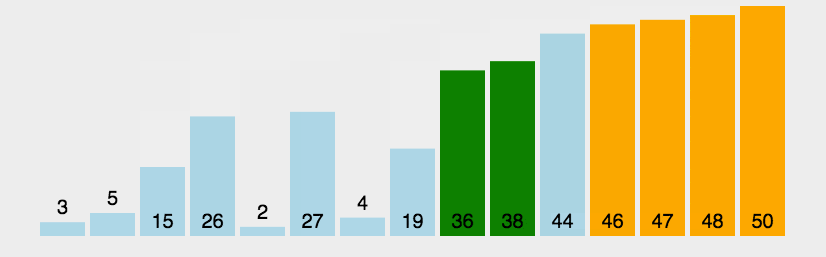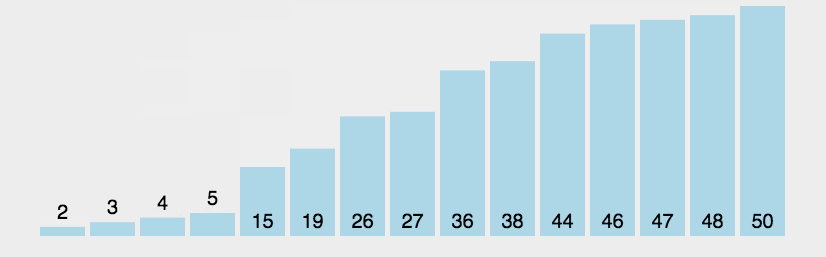
- 代码实现:
func bubleSort(source: inout [Int]) -> [Int] {
print("bubleSort before: \(source)")
for i in 0..<source.count {
for j in i..<source.count {
if source[j]<source[i] {
source.swapAt(i, j)
}
}
}
print("bubleSort after: \(source)")
return source
}
i的循环是计数用,j的循环是当次将最大的数放到最后。
插入排序
- 算法步骤
将第一待排序的第一个元素看过一个有序序列,把第二个元素到最后一个元素当成未排序序列。 从头到位以此扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面)
- 动图演示
由于很好理解就不放动图演示了。
- 代码实现
func insertSort(arr: inout [Int]) {
for i in 1..<arr.endIndex {
let temp = arr[i]
for j in (0..<i).reversed() {
if arr[j] > temp {
arr.swapAt(j, j+1)
}
}
}
}
快速排序
平均状况下,排序n个项目要O(nlogn)次比较。在最坏的状况下则需要O(n^2)次比较,但这种状况并不多见。事实上,快排通常明显比其他O(nlogn)算法更快一个,因为它的内部循环可以在大部分的架构上很有效率地被实现出来。 快排使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。 快速排序本质上是冒泡排序基础上的递归分治法。它是处理大数据排序最快的算法之一了。 《算法艺术与信息学竞赛》上说:
快速排序最坏的情况是O(n^2),比如顺序数列额快排。但它的平摊期望时间是O(nlogn),且O(nlogn)记号中隐含的常数因子很小,比复杂度稳定等于O(nlogn)的归并排序要小很多。所以,对绝大多数树顺序性较弱的随机数列而言,快速排序总是优于归并排序。
- 算法步骤
- 从数列中挑出一个元素,称为“基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准面前,所有比基准大的摆在基准后面(相同的可以放到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归的(recursive)把小于基准值的元素的子数列和大于基准值元素的子数列排序。
- 动图演示
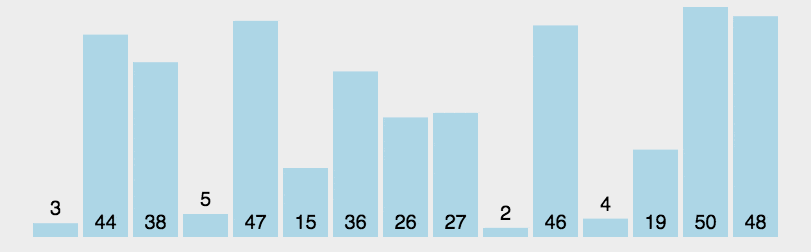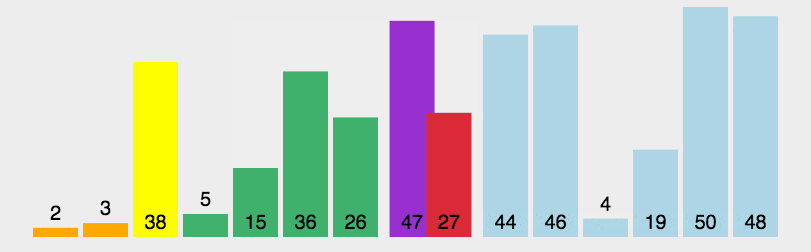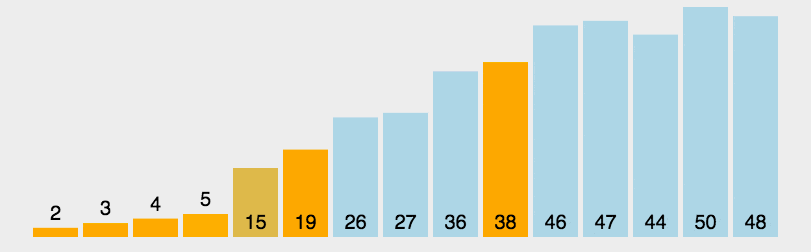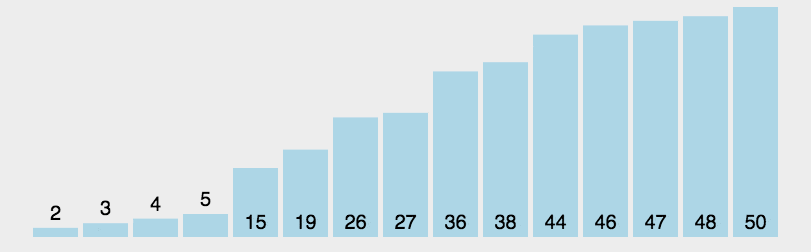
- 代码实现
//寻找pivot的函数
func partition(arr: inout [Int], left: Int, right: Int) -> Int {
let pivot = left
var index = pivot+1
for i in index...right {
if arr[i] < arr[pivot] {
arr.swapAt(i, index)
index+=1
//i和index都更新,以pivot为分隔,两边都冒泡,后面再将假设的pivot替换为真正的pivot,然后继续递归
}
}
//此处相当于pivot需要更新
arr.swapAt(pivot, index-1)
return index-1
}
func quickSort(arr: inout [Int], left: Int, right: Int) {
if arr.count <= 1 {
//nothing, live it alone
}
let left = left
let right = right
if left < right {
let partitionIndex = partition(arr: &arr, left: left, right: right)
quickSort(arr: &arr, left: left, right: partitionIndex-1)
quickSort(arr: &arr, left: partitionIndex+1, right: right)
}
}