LeetCode随笔

这是一篇关于一些LeetCode经典或者热题的随笔记录，旨在保持自己活跃的大脑和思维，要勤思考，多实践

数组/字符串

283.除自身以外数组的乘积

题目

给你一个整数数组 nums，返回数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

题目数据保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位整数范围内。

请不要使用除法，且在 O(n) 时间复杂度内完成此题。

进阶：你可以在 O(1) 的额外空间复杂度内完成这个题目吗？（出于对空间复杂度分析的目的，输出数组不被视为额外空间。）

示例 1:

输入: nums = [1,2,3,4] 输出: [24,12,8,6]

示例 2:

输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]

这似乎是一个简单的问题，可以在线性时间和空间内解决。先计算给定数组所有元素的乘积，然后对数组中的每个元素 xxx，将总的乘积除以 xxx 来求得除自身值的以外数组的乘积。

然而这样的解决方法有一个问题，就是如果输入数组中出现 0，那么这个方法就失效了。而且在问题中说明了不允许使用除法运算。这增加了这个问题的难度。

方法一：左右乘积列表

根据题目的提示，其实对于任何一个位置i的元素，除去它的其他元素的乘积等于前缀之积([0, i-1])乘以后缀之积([i+1, n-1])。所以先不考虑优化的话，可以遍历初始化2个数组，前缀之积数组和后缀之积数组，然后通过多次for循环从而求出最终answer，这样时间复杂度为O(n)，空间复杂度也为O(n)。

func productExceptSelf1(nums: [Int]) -> [Int] {
    let n = nums.count
    
    var left = [Int](repeating: 0, count: n)
    var right = [Int](repeating: 0, count: n)
    
    left[0] = 1
    right[n-1] = 1
    
    for i in stride(from: 1, to: n, by: 1) {
        left[i] = left[i-1] * nums[i-1]
    }
    
    for j in stride(from: n-2, through: 0, by: -1) {
        right[j] = right[j+1] * nums[j+1]
    }

    var rt = [Int](repeating: 0, count: n)
    
    for m in stride(from: 0, to: n, by: 1) {
        rt[m] = left[m] * right[m]
    }
    
    print("leet238: 结果为：\(rt)")

    return rt
}

let c238 = [1,2,3,4] solution.productExceptSelf1(nums: c238)

leet238: 结果为：[24, 12, 8, 6]

方法二：空间复杂度为O(1)

由方法一和题目要求可知，answer数组可以重复利用，所以对于左积数组可以使用answer代替，同样的右积可以不使用数组，直接乘入answer数组即可。

func productExceptSelf2(nums: [Int]) -> [Int] {
    let n = nums.count
    
    var rt = [Int](repeating: 0, count: n)
    
    rt[0] = 1
    
    for i in stride(from: 1, to: n, by: 1) {
        rt[i] = rt[i-1] * nums[i-1]
    }
    
    var right = 1
    
    for j in stride(from: n-1, through: 0, by: -1) {
        rt[j] = right * rt[j]
        
        right = right * nums[j]
    }
    
    print("leet238: 结果为：\(rt)")

    return rt
}

let c238 = [1,2,3,4] solution.productExceptSelf2(nums: c238)

leet238: 结果为：[24, 12, 8, 6]

H指数

题目

274.给你一个整数数组 citations ，其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。

根据维基百科上 h 指数的定义：h 代表“高引用次数” ，一名科研人员的 h 指数是指他（她）至少发表了 h 篇论文，并且至少有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值，h 指数是其中最大的那个。

示例

示例 1：

输入：citations = [3,0,6,1,5] 输出：3 解释：给定数组表示研究者总共有 5 篇论文，每篇论文相应的被引用了 3, 0, 6, 1, 5 次。由于研究者有 3 篇论文每篇至少被引用了 3 次，其余两篇论文每篇被引用不多于 3 次，所以她的 h 指数是 3。

示例 2：

输入：citations = [1,3,1] 输出：1

思路
方法一：排序

首先我们设定初始的H指数为0，然后将引用次数排序，并且对排序后的数组从大到小遍历。根据定义，如果当前值citations[i] > h，则说明我们找到了一篇引用了至少h+1次的论文，所以h+1.继续遍历到h无法继续增大。时间复杂度为O(nlogn)，即排序的时间复杂度，空间复杂度为O(logn)，当然如果该语言不支持直接修改原数组，理论上空间复杂度为O(n)。

func hIndex1(_ citations: [Int]) -> Int {
    var rt = 0
    
    //排序
    var tmp = citations
    
    tmp.sort()
    
    var i = tmp.count - 1

    while i >= 0 && tmp[i] > rt {
        rt = rt + 1
        i = i - 1
    }
    
    print("leet274: \(citations)的h指数为：\(rt)")
    return rt
}

let c274 = [3,0,6,1,5] solution.hIndex1(c274)

leet274: [3, 0, 6, 1, 5]的h指数为：3

方法二：计数排序

根据方法一可知，最终的时间复杂度和空间复杂度都与排序算法有关。所以我们可以用计数排序算法，新建并维护一个数组counter来记录当前应用次数的论文有几篇。

根据定义，我们发现H指数不可能大于总的论文发表数，所以对于引用次数超过论文发表疏导情况，我们可以将其按照总的论文发表数来计算。这样我么可以限制参与排序的数的大小为[0, n]，计数排序的福再度降低到O(n)。最后，我们从后向前遍历数组counter（counter每个元素表明的是该引用次数的论文有几篇，如第i个元素的值表明为引用为i次数的文章有几篇），在counter中，如果得到 >= 当前引用次数i的总论文数，则为h指数。注意counter的长度为原数组count+1，因为可能有论文被引用0次。时间复杂度为O(n)，空间复杂度为O(n)。

func hIndex2(citations: [Int]) -> Int {
    let n = citations.count
    
    var counter = [Int](repeating: 0, count: n + 1)
    
    //初始化counter
    for item in citations {
        counter[min(n, item)] += 1
    }
    
    var rt = 0
    
    for i in stride(from: n, through: 0, by: -1) {
        rt += counter[i]
        
        if rt >= i {
            break
        }
    }
    
    print("leet274: \(citations)的h指数为：\(rt)")

    return rt
}

let c274 = [3,0,6,1,5] solution.hIndex2(citations: c274)

leet274: [3, 0, 6, 1, 5]的h指数为：3

跳跃游戏II

题目

45.给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

0 <= j <= nums[i] i + j < n 返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例

示例 1:

输入: nums = [2,3,1,1,4] 输出: 2 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4] 输出: 2

思路

这道题是典型的贪心算法，通过局部最优解得到全局最优解。 注意，题目保证了可以到达 nums[n - 1]

方法一：反向查找

我们的目标是到达数组的最后一个位置，所以我们可以考虑最后一步跳跃前所在的位置，改位置通过跳跃能够到达最后一个位置，有点像爬楼梯（斐波拉契数列）反过来想一样，如果有多个位置可以通过跳跃到达最后一个位置，那么我们如何选择呢？可以 贪心 地选择距离最后一个位置最远的那个位置，也就是对应下标最小的那个位置。找到最后一步跳跃之前所在的位置后，我们继续贪心地寻找倒数第二步跳跃前所在的位置，以此类推，直到找到数组的开始位置。时间复杂度为O(n2)，空间复杂度为O(1)。

func canJump2(nums: [Int]) -> Int {
    let len = nums.count
    
    if len <= 0 {
        return 0
    }
    
    //最小步数
    var rt = 0
    
    var position = len - 1
    
    while position > 0 {
        for i in 0 ..< position {
            if i + nums[i] >= position {
                //说明能到达，更新position，同时步数也要+1，然后去找更前面一个position
                position = i
                rt = rt + 1
                break
            }
        }
    }
    
    print("leet45: 最小跳跃次数为：\(rt)")
    
    return rt
}

let nums3 = [2,3,1,1,4] let _ = solution.canJump2(nums: nums3)

leet45: [2, 3, 1, 1, 4]的最小跳跃次数为：2

方法二：正向贪心

如果我们贪心地正向查找，每次找到可到达的最远位置，就可以在线性时间内得到最少跳跃次数。例如，对于数组[2,3,1,2,4,2,3]，初始下标为0，从0开始出发，最远可以到达下标2。下标0可到达的位置中，下标1的值是3，从下标1出发可以到达更远的位置，因此第一步到达下标1。从下标1出发，最远可以到达下标4.下标1可到达的位置中，下标4的值是4，从下标4可以到达更远的位置，因此第二步到达下标4. 在具体的实现中，我们维护当前能到达的最大下标位置，记为边界。从左到右遍历数组，到达边界时，更新边界并将跳跃跌的次数+1. 在遍历数组时，我们不访问最后一个元素，因为在访问最后一个元素之前，我们的边界一定>=最后一个位置了。如果访问最后一个元素，在边界正好为最后一个位置的情况下，我们会增加一次不必要的跳跃次数，因此我们不必访问最后一个元素。

func canJump3(nums: [Int]) -> Int {
    let len = nums.count
    
    if len <= 0 {
        return 0
    }
    
    var maxPosition = 0
    var end = 0
    var rt = 0
    
    for i in 0 ..< len-1 {
        maxPosition = max(maxPosition, i + nums[i])
        
        if i == end {
            end = maxPosition
            rt = rt + 1
        }
    }
    
    print("leet45: \(nums)的最小跳跃次数为：\(rt)")

    return rt
}

let nums3 = [2,3,1,1,4] let _ = solution.canJump3(nums: nums3)

leet45: [2, 3, 1, 1, 4]的最小跳跃次数为：2

跳跃游戏

题目

55.给你一个非负整数数组 nums ，你最初位于数组的第一个下标。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例

示例 1：输入：nums = [2,3,1,1,4] 输出：true 解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：输入：nums = [3,2,1,0,4] 输出：false 解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ，所以永远不可能到达最后一个下标。

思路

可以采用贪心算法，对于数组中的任意一个位置 y，如何判断它能到达？只要存在一个位置 x，它本身可以到达，并且它跳跃的最大长度为 x + nums[x]，这个值 >= y，即 x + nums[x] >= y，那么 y 也可以到达。在遍历的过程中，如果最远可以到达的位置 >= 数组中的最后一个位置，则说明最后一个位置可以到达，返回true，反之，如果遍历结束后，最后一个位置仍不可达，返回false。

简单来说： 1.如果某一个作为起跳点的格子可以跳跃的距离是 3，那么表示后面 3 个格子都可以作为起跳点 2.可以对每一个能作为起跳点的格子都尝试跳一次，把能跳到最远的距离不断更新 3.如果可以一直跳到最后，就成功了时间复杂度为O(n)，空间复杂度为O(1)。

func canJump(nums: [Int]) -> Bool {
    //rightmost表示能跳到的最远距离
    var rightmost = 0;
    let len = nums.count
        
    for i in 0..<len {
        //首先要确保能到达的最右边是可以到达i位置，然后在次基础上更新rightmost，取max，再然后rightmost还能大于右边边界，即能到达
        if rightmost >= i {
            rightmost = max(rightmost, i + nums[i])
            
            //再然后的判断
            if rightmost >= len - 1 {
                print("\(nums) 可以跳到数组最后一个元素：true")
    
                return true
            }
        }
    }
        
    print("\(nums) 可以跳到数组最后一个元素：false")
    
    return false
}

  let nums2 = [3,2,1,0,4]
  let _ = solution.canJump(nums: nums2)
[3, 2, 1, 0, 4] 可以跳到数组最后一个元素：false

删除有序数组中的重复项 II

题目

80：给你一个有序数组 nums ，请你原地删除重复出现的元素，使得出现次数超过两次的元素只出现两次，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。

示例

输入：nums = [1,1,1,2,2,3] 输出：5, nums = [1,1,2,2,3] 解释：函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3。不需要考虑数组中超出新长度后面的元素。

输入：nums = [0,0,1,1,1,1,2,3,3] 输出：7, nums = [0,0,1,1,2,3,3] 解释：函数应返回新长度 length = 7, 并且原数组的前七个元素被修改为 0, 0, 1, 1, 2, 3, 3。不需要考虑数组中超出新长度后面的元素。

思路

首先，非严格递增的数组nums，则和之前一样，后面的元素必然 >= 前面的元素，由于题目要求出现次数超过两次的元素只保留两次，且空间复杂度为O(1)，所以采用双指针法。由于相同的元素必然是连续的，假设有一段连续相同的number，所以会从第3个相同元素可以替换，前面2个保留下来。根据26题的思路，nums[fast]和nums[slow-2]不同时，nums[fast]需要被替换，也就是更新为slow，slow表明是需要被替换的位置，fast是遍历的位置。时间复杂度为O(n)，空间复杂度为O(1)。

func removeDuplicates3(nums: inout [Int]) -> Int {
    let len = nums.count
    
    if len <= 2 {
        return len
    }
    
    var rt = 0
    
    var slow = 2
    
    //slow是需要替换的位置，那么slow-2自然就是需要保留的位置
    for fast in 2..<len {
        if nums[fast] != nums[slow - 2] {
            nums[slow] = nums[fast]
            slow = slow + 1
        }
    }
            
    rt = slow
    
    print("不同的元素数组是3：\(nums) num is: \(rt)")
    
    return rt
}

var nums = [0,0,1,1,1,1,2,3,3] let _ = solution.removeDuplicates3(nums: &nums)

不同的元素数组是3：[0, 0, 1, 1, 2, 3, 3, 3, 3] num is: 7

删除有序数组中的重复项

题目

26：给定一个非严格递增排列的数组nums，请你原地删除重复出现的元素，使每个元素只出现一次，返回删除后的数组的新长度，元素的相对顺序应该保持一致，然后返回nums中唯一元素的个数。

示例

输入：nums = [1,1,2] 输出：2, nums = [1,2] 解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

输入：nums = [0,0,1,1,1,2,2,3,3,4] 输出：5, nums = [0,1,2,3,4] 解释：函数应该返回新的长度 5 ，并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

思路

暴力法

不考虑时间和空间问题，由于数组已经排过需了，那么只需要一个指针循环旧数组，一个新数组，第一个元素肯定放入新数组，然后从第二个元素开始遍历到旧数组结尾，如果和第一个元素相同则跳过，不同则记录入新数组，最后将新数组放入老数组即可，也可不放入。如果旧数组为空，不处理，长度＜＝2，则肯定是原数组了，直接返回原数组个数。时间复杂度为O(n)，空间复杂度为O(n)。

  func removeDuplicates1(_ nums: inout [Int]) -> Int {
      if nums.count < 2 {
          return nums.count
      }
        
      var rt = 0
        
      var tmpArr = [Int]()
        
      var tmp = nums[0]
        
      tmpArr.append(tmp)
        
      for i in 1..<nums.count {
          if nums[i] > tmp {
              //说明不同，否则至少相等，因为已经排过序
              tmp = nums[i]
              tmpArr.append(tmp)
          }
      }
        
      rt = tmpArr.count
        
      print("不同的元素数组是1：\(tmpArr)")
        
      return rt
  }

var nums = [0,0,1,1,1,2,2,3,3,4] let _ = solution.removeDuplicates1(&nums)

不同的元素数组是：[0, 1, 2, 3, 4]

双指针法

由于数组是排过序的，后面的元素只可能存在等于或者大于前一个元素两种状态，由于可以改变原数组，所以所有重复位置的元素都可以被后来不重复的元素替换，所以可以定义快慢2个指针，快指针用于扫描，找出不同的元素，慢指针指向可以替换的位置（也就是重复元素的位置）时间复杂度为O(n)，空间复杂度为O(1)。

  func removeDuplicates2(nums: inout [Int]) -> Int {
      if nums.count < 2 {
          return nums.count
      }
        
      var rt = 0
        
      //直接从第二个元素开始遍历
      var slow = 1
        
      for fast in 1..<nums.count {
          if nums[fast] > nums[slow-1] {
              nums[slow] = nums[fast]
              slow = slow + 1
          }
      }
        
      rt = slow
        
      print("不同的元素数组是2：\(nums) num is: \(rt)")

      return rt
  }

var nums = [0,0,1,1,1,2,2,3,3,4] let _ = solution.removeDuplicates2(nums: &nums)

不同的元素数组是2：[0, 1, 2, 3, 4, 2, 2, 3, 3, 4] num is: 5

接雨水

题目

42：给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水，如下所示：

rain

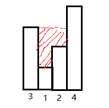
上图中，盛水量为3.

示例

输入：height = [3,1,2,4]
输出：3

思路

暴力法

每个i位置，都前后遍历，从i位置向前和向后遍历，找到前后max值较小的减去当前i位置的值就是能装的水，要是前或者后没有找到比i位置小的，那么就不能装水，复杂度为O(n2)

  //柱状图接水(暴力法)
  func getWaterByViolence(src: [Int]) -> Int {
      var rt = 0
        
      if src.isEmpty || src.count < 3 {
          return rt
      }
        
        
      for i in 1..<src.count-1 {
          var leftMax = src[0]
            
  //        获取作则最大值
          for j in 0..<i {
              if src[j] > leftMax {
                  leftMax = src[j]
              }
          }
            
  //        获取右侧最大值
          var rightMax = src[src.count-1]
            
          for k in (i+1...src.count-1).reversed() {
              if src[k] > rightMax {
                  rightMax = src[k]
              }
          }
            
  //        左右两个大值中的较小者和src[i]的差值就是当条柱状图所能储水的值
  //        且如果他们都比src[i]小的话就储不了水
          rt += max(0, min(leftMax, rightMax) - src[i])
      }
        
      print("\(src)'s 柱状图接水(暴力法) is \(rt)")
    
      return rt
  }

控制台

let _ = getWaterByViolence(src: [3, 1, 2, 4])

[3, 1, 2, 4]’s 柱状图接水(暴力法) is 3

双指针法

定义一个双指针，分别为左右指针，分别指向arr[1]和arr[count-2]，因为第一个和最后一个肯定不能储水，同时定义2个最值，leftMax和rightMax分别为第二个元素和倒数第二个元素。当左最值小于右最值时，右滑左指针，左指针上能储的水就是：左最值＞左指针，相减，左最值<左指针，不减，更新左最值；同样的逻辑对于左最值大于右最值时，也来一遍。时间复杂度为O(n),空间复杂度为O(1)

          //柱状图接水(左右指针法)，时间复杂度O(n2)，空间复杂度O(1)
      func getWaterBy2P(arr: [Int]) -> Int {
          var rt = 0
            
          if arr.isEmpty || arr.count < 3 {
              return rt
          }
            
          var leftMax = arr[0]
          var rightMax = arr[arr.count-1]
            
          var leftP = 1
          var rightP = arr.count-2
            
          while leftP <= rightP {
              if leftMax <= rightMax {
      //            rt += leftMax-arr[leftP] > 0 ? leftMax-arr[leftP] : 0
                  rt += max(0, leftMax-arr[leftP])
                  leftMax = max(leftMax, arr[leftP])
                    
                  leftP+=1
              } else {
      //            rt += rightMax-arr[rightP] > 0 ? rightMax-arr[rightP] : 0
                  rt += max(0, rightMax-arr[rightP])
                  rightMax = max(rightMax, arr[rightP])
                    
                  rightP -= 1
              }
          }
            
          print("\(arr)'s 柱状图接水(左右指针法) is \(rt)")
        
          return rt
      }

控制台

let _ = getWaterBy2P(arr: [3, 1, 2, 4])

[3, 1, 2, 4]’s 柱状图接水(左右指针法) is 3

上篇并查集

下篇偶来无聊, 拙笔涂鸦几首