一些算法举例
动态规划
Triangle
给定一个三角形数组,找到从上到下最小的sum的路径
示例:
[2]
[3, 4]
[6, 5, 7]
[4, 1, 8, 3]
最小的path sum is 11(i.e. 2+3+5+1=11)
解析
-
暴力法 采用递归的方式:走到最后一行最后一个元素肯定是它肩部走过来的,也就是它left肩orright肩
代码如下:
/* *给定一个三角形数组,找到从上到下最小的sum的路径 *[2] *[3, 4] *[6, 5, 7] *[4, 1, 8, 3] *最小的path sum is 11(i.e. 2+3+5+1=11) */ func minimumTotal(_ triangle: [[Int]]) -> Int { var path = "" var rlt = minimumTotalHelper(triangle, 0, 0, &path) print("rls is \(rlt)") return rlt; } func minimumTotalHelper(_ triangle: [[Int]], _ row: Int, _ col: Int, _ path: inout String) -> Int { //terminator if row == triangle.count - 1 { return triangle[row][col] } //process //drill down let left = minimumTotalHelper(triangle, row+1, col, &path) let right = minimumTotalHelper(triangle, row+1, col+1, &path) //clear states //no need here return triangle[row][col] + min(left, right) } ============ let triangle = [ [2], [3, 4], [6, 5, 7], [4, 1, 8, 3], ] let _ = minimumTotal(triangle) rls is 11 -
- DP法
- 换个思路想一下,从上到下走到了最小,那么反过来从下向上这条链路也肯定是最短的
- 所以
- 状态定义为:
- dp[j]:表明从到这个节点的最短距离
- 初始状态:最后一行
- 状态转移方程:
- dp[j] = target[i][j]+min{dp[j], dp[j+1]}
- i是倒过来,从row-2到0
- j是0…i
代码如下:
/* *给定一个三角形数组,找到从上到下最小的sum的路径 *[2] *[3, 4] *[6, 5, 7] *[4, 1, 8, 3] *最小的path sum is 11(i.e. 2+3+5+1=11) */ func minimumTotalByDP(_ triangle: [[Int]]) -> Int { let rows = triangle.count //由于最后一行是最长的,三角矩阵的特点 var dp = triangle.last! for i in stride(from: rows - 2, through: 0, by: -1) { for j in 0...i { print("minimumTotalByDP is \(triangle[i][j]) \(dp[j]) \(dp[j+1])") dp[j] = triangle[i][j] + min(dp[j], dp[j+1]) print(dp) } } print("minimumTotalByDP is \(dp[0])") return dp[0] }
MinEditDistance
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
解析
使用动态规划的方式:
1.状态定义:
word1长度为m, word2长度为n, 尝试用一维的dp,状态不够,无法表述状态,所以升维,变成二维
dp[i,j]表示word1的前i个字符变成word2的前j个字符所需要的最少步骤
2.状态方程:
If:word[i]==word[j]表明i,j这一位不需要动,直接赋值给dp[i,j]即可
else:要不word1删除一个字符匹配,要不word2删除一个字符匹配,要不两个都需要变动(replace),取这三种方式的最小的一个dp,加上最后一次操作(+1)
Min{dp[i,j-1], dp[i-1,j], dp[i-1, j-1]}+1
代码
extension String {
subscript(_ i: Int)->Character {
get {return self[index(startIndex, offsetBy: i)]}
}
}
/*
*Edit Distance
*word1(m)->word2(n)需要的最短步骤
*horse->ros, intention->nation
*/
func minEditDistanc(word1: String, word2: String) -> Int {
var result = -1;
let m = word1.count
let n = word2.count
//Initial the two-dimension array
var dp = [[Int]](repeating: [Int](repeating: 0, count: n+1), count: m+1)
for i in 0...m {
//第一个单词前面的i个字符,第二个单词有0个字符,那需要匹配多少个次呢?当然是第一个i个字符全部删除
dp[i][0]=i
}
//同理
for j in 0...n {
dp[0][j]=j
}
for i in 1...m {
for j in 1...n {
if word1[i-1]==word2[j-1] {
dp[i][j]=dp[i-1][j-1]
} else {
//+1是肯定需要操作一次,然后是取3个中间的最小值:删除word2的j,删除word1的i个字符,两个都需要删除,重新替换
//这就是这3个比较的由来,由于是轮换对称的,不必纠结删除哪个,新增另一个word的字符,等价的
dp[i][j]=1+min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1])
}
}
}
result=dp[m][n]
print("minEditDistanc in \(word1) & \(word2) is: \(result)")
return result;
}
===========================
let word1 = "horse"
let word2 = "ros"
// let word1 = "intention"
// let word2 = "execution"
let _ = minEditDistanc(word1: word1, word2: word2)
===========================
minEditDistanc in horse & ros is: 3
零钱兑换
有若干面值的硬币,如:[1,6,7] , 求组成特定面值,如:30,的最小硬币数。
-
示例
输入:[1,6,7] 30 输出:5(6*5) 输入:[1,2,5] 11 输出:3(5*2,1)和上楼梯的有最少步数本质上是一样的。
-
解析
采用动态规划的方式: 状态定义:dp[i]—上到第i层楼梯(面值)的最少步数 状态转移:dp[i]=min{dp[i-coins[j]]}+1—j:0->n-1 第i层减去最后一个面值(+的1)的最少步数
两层循环:for: i(0…x)
for:j(0..<n)
-
代码
/* *零钱兑换:有若干面值的硬币,如:[1,6,7] , 求组成特定面值,如:30,的最小硬币数。 *类似到达特定楼层比如30层,step可选1,6,7,最少需要多少次 */ func coinsChangeOrGotoFloorMinStep(coins: [Int], change: Int) -> Int { var result = -1 if coins.count<=0 || change<=0 { return result } var DP = [Int](repeating: Int.max, count: change+1) DP[0] = 0 for i in 1...change { for j in 0..<coins.count { if i>=coins[j] { DP[i]=min(DP[i], DP[i-coins[j]]+1) } } } if DP[change]>0 { result=DP[change] print("coinsChangeOrGotoFloorMinStep is: \(result)") return result } print("coinsChangeOrGotoFloorMinStep cannot be found") return result; } -
结果
let coins = [1,6,7] let _ = coinsChangeOrGotoFloorMinStep(coins: coins, change: 30) ========================LeetCode: DynamicProgramingCode========================= coinsChangeOrGotoFloorMinStep is: 5
买卖股票的最佳时机
给定一个数组,它的第i个元素是一支给定股票第i天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票一次),设计一个算法来计算你所能获取的最大利润。
注意: 你不能再买入股票前卖出股票。
- 示例
输入:[7,1,5,3,6,4]
输出: 5
解释: 在第2天(股票价格=1)的时候买入,在第5天(=6),最大利润=6-1=5.注意利润不可能是7-1
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下,没有交易完成,所以利润为0.
- 思路
需要找到最小的谷之后的最大的峰。 我们可以维持两个变量——minprice 和 maxprofit,它们分别对应迄今为止所得到的最小的谷值和最大的利润(卖出价格与最低价格之间的最大差值)。
- 解法
func maxProfit(_ prices: [Int]) -> Int {
var minPrice = Int.max
var maxProfit = 0
for i in 0..<prices.count {
if prices[i] < minPrice {
minPrice = prices[i]
} else if prices[i] - minPrice > maxProfit {
maxProfit = prices[i]-minPrice
}
}
return maxProfit
}
- 结果
print(solution.maxProfit([7,1,5,3,6,4]))
5
买卖股票的最佳时机II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
- 示例
输入:[7,1,5,3,6,4]
输出:7
解释:在第2天(=1)买入,第三天(=5)卖出,利润4,然后在第4天(=3)买入,第5天(=6)卖出,利润3
总利润3+4=7
- 思路
在斜坡上爬升并持续增加从交易中获得的利润
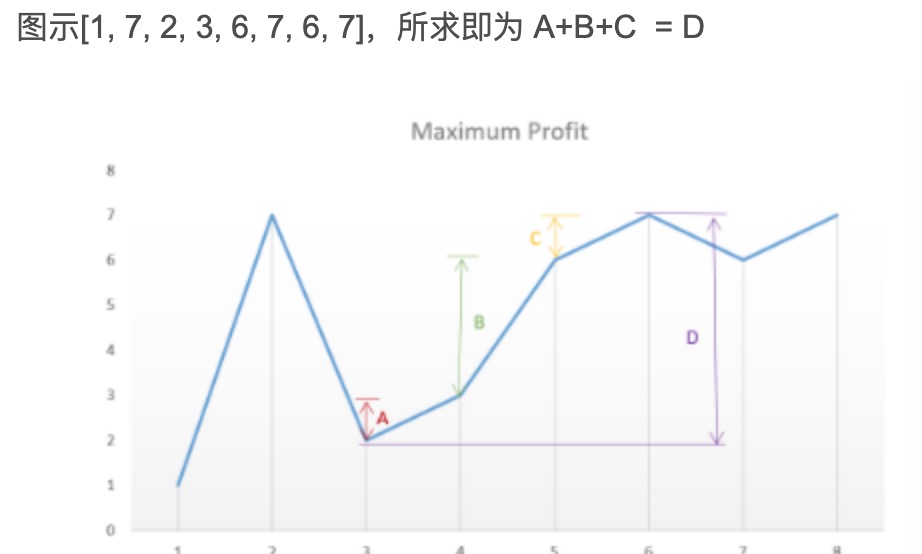
- 解法
func maxProfitII(_ prices: [Int]) -> Int {
if prices.count < 2 {
return 0
}
var maxProfit = 0
for i in 1..<prices.count {
if prices[i] > prices[i-1] {
maxProfit += prices[i]-prices[i-1]
}
}
return maxProfit
}
- 结果
print(solution.maxProfitII([7,1,5,3,6,4]))
7
滑动窗口最大值
给定一个Int窗口,实时的输出窗口最大的元素
- 示例
输入:k=3,nums=[1,3,-1,-3,5,3,6]
输出:[3,3,5,5,6]
- 思路
窗口为3个位置,只要有一个最大值进来,比他早的元素永远没有出头之日,所以可以直接忽略掉。
- 解法
func findMaxInWindow(_ count: Int, _ nums: [Int]) -> [Int] {
var res = [Int]()
if nums.count < 0 {
return []
}
var maxNum = Int.min
if nums.count < count {
for i in 0..<nums.count {
if nums[i] > maxNum {
maxNum = nums[i]
}
}
res.append(maxNum)
return res
}
for i in 0..<count {
if nums[i] > maxNum {
maxNum = nums[i]
}
}
res.append(maxNum)
for j in (nums.count-count-1)..<nums.count {
if nums[j] > maxNum {
maxNum = nums[j]
}
res.append(maxNum)
}
return res
}
- 结果
let r15 = solution.findMaxInWindow(3, [1,3,-1,-3,5,3,6])
print(r15)
[3, 3, 5, 5, 6]
生成小括号字符串
给定固定长度,比如n,生成所有合法的小括号组成形式
- 示例
输入: n=3
输出: ["((()))", "(()())", "(())()", "()(())", "()()()"]
- 思路
采用递归,但是要注意,左右括号肯定都是为n个,并且左括号可以随意加(不超过n),但是右括号必须要在左括号大于右括号的时候才可以输入,然后递归即可
- 解法
func generateParenthesis(_ count: Int) -> [String] {
var res: [String] = [String]()
_gen(0, 0, count, "", &res)
return res
}
func _gen(_ left: Int, _ right: Int, _ count: Int, _ result: String, _ res: inout [String]) {
//递归出口
if left == count && right == count {
res.append(result)
}
if left < count {
_gen(left+1, right, count, result+"(", &res)
}
if left > right && right < count {
_gen(left, right+1, count, result+")", &res)
}
}
- 结果
let r16 = solution.generateParenthesis(3)
print(r16)
[”((()))”, “(()())”, “(())()”, “()(())”, “()()()”]
最小路径问题
一个Int型的二维数组(m*n),>0,每个值表明距离,左上角记为【0,0】,右下角记为【m,n】,每个数字只能向右或者向下进行,求出从【0,0】->【m,n】的最小路径。
- 示例
输入(Path):
| 1 | 1 | 3 |
| 2 | 3 | 2 |
| 5 | 1 | 2 |
| 10 | 1 | 5 |
输出:
1-1-3-1-1-5 = 12(最短路径)
- 思路
采用DP的方式。 状态定义:建立一个同维状态数组DP,相应的位置表示到达此位置的最短路径,如DP[i][j]表示到达Path[i][j]的最短路径; 状态转移方程:DP[0][0]没有选择,肯定就是等于Path[0][0],由于只能向右或者向左行进,所以DP[i][j]只能从Path[i][j-1]或者Path[i-1][j]这两个节点过来的,而当下Path[i][j]的值是固定的。所以DP[i][j]=min{DP[i][j-1], DP[i-1][j]}+Path[i][j]
注:DP[i][j-1]存放的就是到达Path[i][j-1]的最小路径值
第一行和第一列都是比较特殊的存在,只需要累加即能得出路径,如:DP[0][j]=DP[0][j-1]+Path[0][j]
- 实现
/*
*一个Int型的二维数组(m*n),>0,每个值表明距离,左上角记为【0,0】,右下角记为【m,n】,每个数字只能向右或者向下进行,求出从【0,0】->【m,n】的最小路径。
*/
func findMinimumPath(inPath path: [[Int]]) -> Int {
if path.count<=0 {
return -1
}
var DP=[[Int]](repeating: [Int](repeating: 0, count: path[0].count), count: path.count)
var rls=DP[0][0];
var row=path[0][0]
//初始化第一行DP
for j in 1..<path[0].count {
DP[0][j]=row+path[0][j]
row=DP[0][j]
}
var col=path[0][0]
//初始化第一列DP
for i in 1..<path.count {
DP[i][0]=col+path[i][0]
col=DP[i][0]
}
//初始化剩余部分
for i in 1..<path.count {
for j in 1..<path[i].count {
DP[i][j]=min(DP[i-1][j], DP[i][j-1])+path[i][j]
rls=DP[i][j]
}
}
print("findMinimumPath is: \(rls)")
return rls;
}
- 结果
let path=[
[1, 1, 3],
[2, 3, 2],
[5, 1, 2],
[10, 1, 5],
]
let _=findMinimumPath(inPath: path)
> findMinimumPath is: 12