一些算法举例
树
树是最常用且非常有用的数据结构之一,通过下图可以很容易理解树的概念。
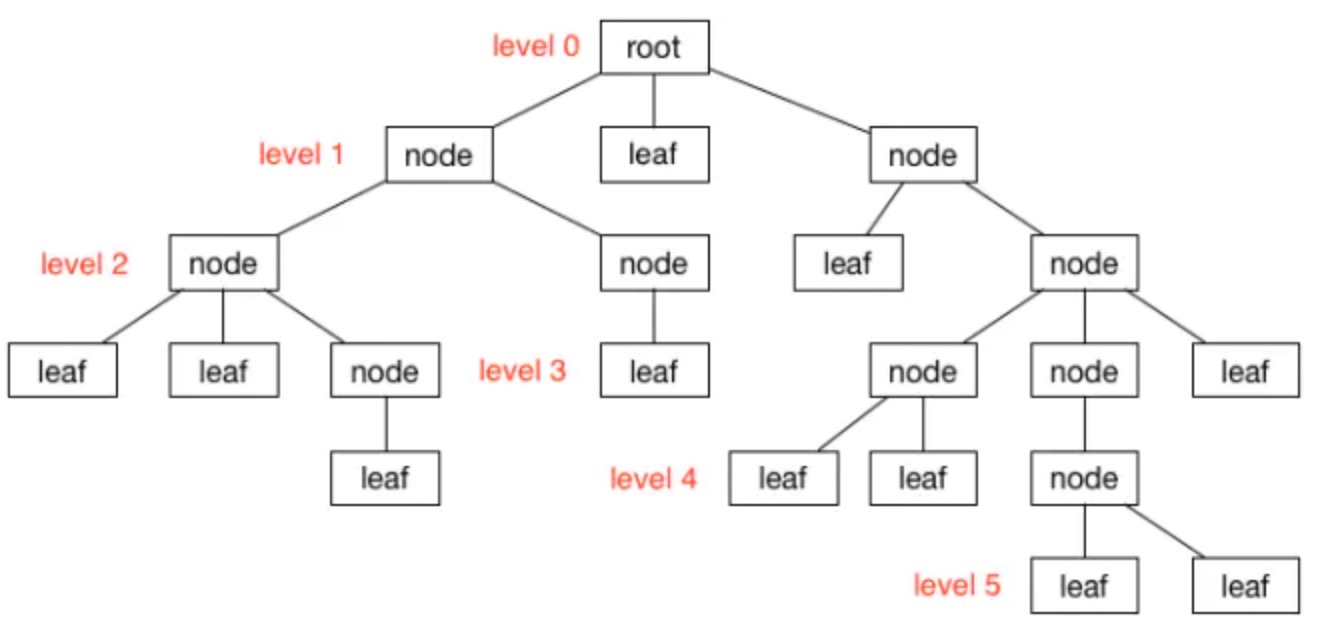
上图展示的是一个拥有5个层级数的树结构。树根root是第0层,从树最外层开始每深入一层,其层级树相应的减1。 树能帮你解决很多问题,包括:
- 表示对象的层级关系
- 使查询快速高效
- 能提供有序的数据链
- 文本的前缀匹配搜索
swift构造树
class TreeNode<T> {
var value: T
var children: [TreeNode] = []
weak var parent: TreeNode?
init(value: T) {
self.value = value
}
func add(child: TreeNode) {
children.append(child)
child.parent = self
}
}
但是这种是没办法被print打印出来的。需要:
extension TreeNode: CustomStringConvertible {
var description: String {
var text = "\(value)"
if !children.isEmpty {
text += "{"+children.map{$0.description}.joined(separator: ", ")+"}"
}
return text
}
}
搜索:
extension TreeNode where T: Equatable {
func search(value: T) -> TreeNode? {
if value == self.value {
return self
}
for child in children {
if let found = child.search(value: value) {
return found
}
}
return nil
}
}
为数组建立二进制搜索树,并搜索范围内的节点
- 示例:
输入:int型数组[7, 20,9,10,25,16,2,40,16,6]
范围:[9,35]
输出:9,10,20, 25, 16
-
思路:
-
构建BST:
class BinaryTree<T: Comparable> {
public var value: T
public var parent: BinaryTree?
public var left: BinaryTree?
public var right: BinaryTree?
init(value: T) {
self.value = value
}
var isRoot: Bool {
return parent == nil
}
var isLeaf: Bool {
return left == nil && right == nil
}
var isLeftChild: Bool {
return parent?.left === self
}
var isRightChild: Bool {
return parent?.right === self
}
var hasLeftChild: Bool {
return left != nil
}
var hasRightChild: Bool {
return right != nil
}
var hasBothChildren: Bool {
return hasLeftChild && hasRightChild
}
var count: Int {
return (left?.count ?? 0)+1+(right?.count ?? 0)
}
}
class BinarySearchTree<T: Comparable> : BinaryTree<T> {
func insert(value: T) {
if value < self.value {
if hasLeftChild {
(left as! BinarySearchTree).insert(value: value)
} else {
left = BinarySearchTree(value: value)
left?.parent = self
}
} else {
if hasRightChild {
(right as! BinarySearchTree).insert(value: value)
} else {
right = BinarySearchTree(value: value)
right?.parent = self
}
}
}
}
- 功能函数:
//获取[9,35]
func findTree(tree: BinarySearchTree<Int>) {
if tree.value <= 9 {
//在右边找
if tree.value == 9 {
print(tree.value, terminator: " ")
}
if tree.hasRightChild {
findTree(tree: tree.right!)
}
} else if tree.value >= 35 {
//在左边找
if tree.value == 35 {
print(tree.value, terminator: " ")
}
if tree.hasLeftChild {
findTree(tree: tree.left!)
}
} else if tree.value > 9 && tree.value < 35 {
print(tree.value, terminator: " ")
if tree.hasLeftChild {
findTree(tree: tree.left!)
}
if tree.hasRightChild {
findTree(tree: tree.right!)
}
}
}
- 测试:
let tree = BinarySearchTree<Int>(value: 7)
tree.insert(value: 20)
tree.insert(value: 9)
tree.insert(value: 10)
tree.insert(value: 25)
tree.insert(value: 16)
tree.insert(value: 2)
tree.insert(value: 40)
tree.insert(value: 16)
tree.insert(value: 6)
print(tree)
(2 -> (6)) <- 7 -> ((9 -> (10 -> (16))) <- 20 -> (25 -> (40)))
20 9 10 16 25
输出一颗树所有的到叶子节点的路径
- 示例:
输入:int型数组[7, 20,9,10,25,16,2,40,16,6]
输出:["7->2->6", "7->20->9->10->16", "7->20->25->40"]
-
思路 很简单,递归,先去实现左子树的路径,而后实现右子树的路径
-
实现 沿用上述的二叉搜索树结构(自定义的二叉树结构也测试过,此处不展示了)
public func outputAllPathInBTree(root: BinaryTree<Int>?, path: String, paths: inout [String]) -> Void { if root == nil { return } var p = path.appending(String(root!.value)) if root?.left == nil && root?.right == nil { paths.append(p) } else { p = p.appending("->") outputAllPathInBTree(root: root?.left, path: p, paths: &paths) outputAllPathInBTree(root: root?.right, path: p, paths: &paths) } } -
测试
let bsTree = generateBSTree() let bTree = generateBTree() let bstpath = "" var bstpaths: [String] = [] outputAllPathInBTree(root: bsTree, path: bstpath, paths: &bstpaths) print("outputAllPathInBTree is: ") print(bstpaths) public func generateBTree() -> BinaryTree<Int> { let bTree = BinaryTree(value: 1) bTree.right = BinaryTree(value: 3) let bl = BinaryTree(value: 2) bl.right = BinaryTree(value: 5) bTree.left = bl print("binary tree is: ") print(bTree) print("\r") return bTree }
outputAllPathInBTree is: [“7->2->6”, “7->20->9->10->16”, “7->20->25->40”]
outputAllPathInBTree is: [“1->2->5”, “1->3”]